Recursive functions can be a bit mindbending when you first encounter them. As part of my process to understand them better I looked at some simple examples and tried to step through each function stage by stage to get an idea of how the seemingly paradoxical process of a function calling itself can actually return a result. My intial way into this was through the “bubbling up” analogy, which really intuitive and easy to grasp. Once that makes sense, there’s a refinement to the analogy which looks at the way the call stack manages function calls when a script is being run in browser.
Check out this example of a really simple recursive function:
function factorial(n){
if (n === 1){
return 1;
{
else {
return n * factorial (n-1);
}
}
The function factorial(n) simply calculates n!, factorial of the integer n, which can be found by evaluating n * (n-1) * (n-2) * (n-3) ... * 1. There are ways to evaluate the factorials of 0 and of minus numbers, but for simplicity this function will only work as long as n>=1.
Clearly theres a lot of repetition required to evaluate a factorial, and that’s why it makes sense to write it as a recursive function. Just like all recursive functions this one includes a recursive condition (the condition under which it will call itself again, creating a loop) and a break condition (the condition where the function eventually terminates, breaking out of the loop). Here, the break condition is met when n === 1 since there are no more integers left to multiply after this.
Plugging in a value and stepping through the function in your head might go something like this:
console.log(factorial(5))
↓
//5 != 0 so ignore the break condition
↓
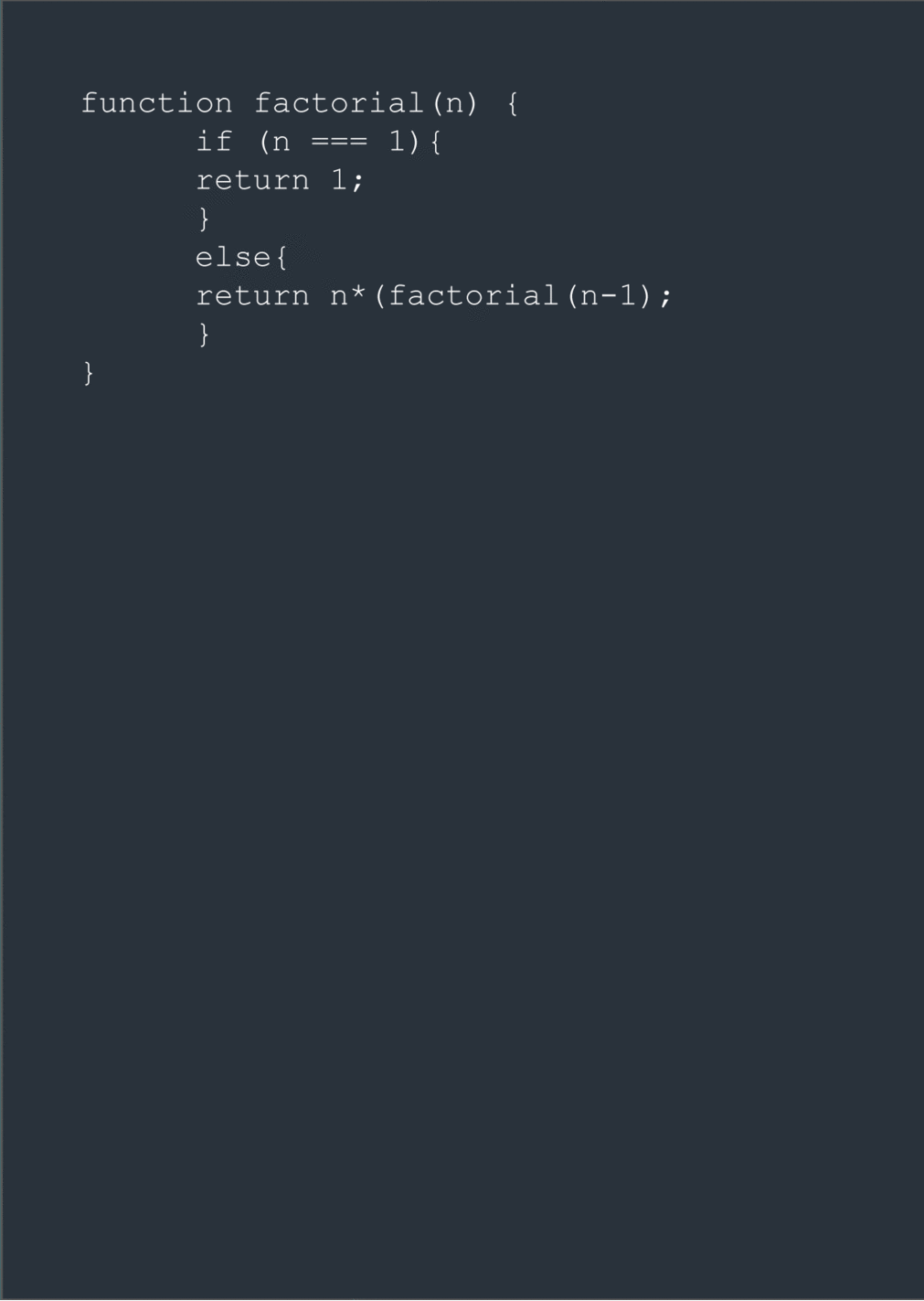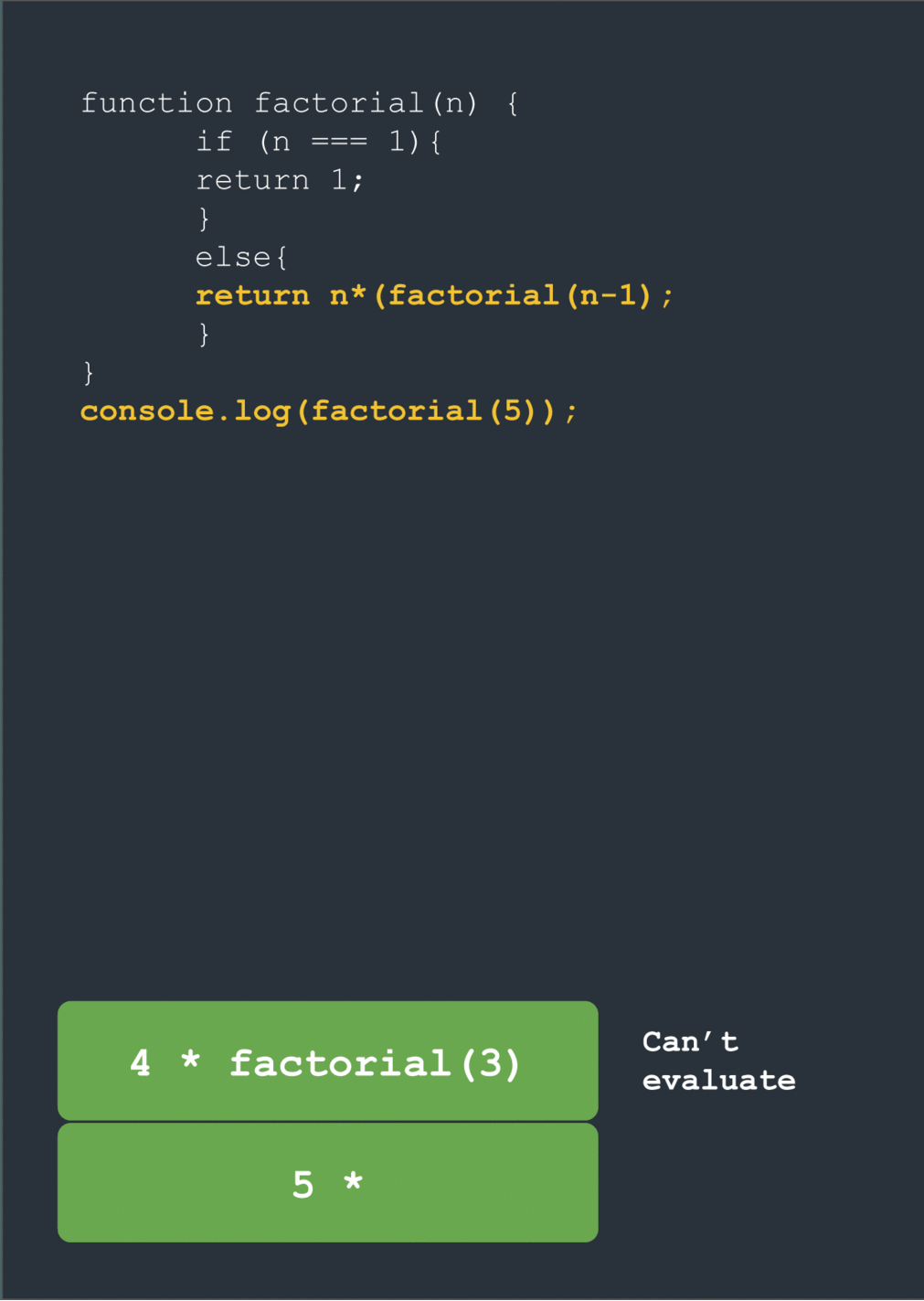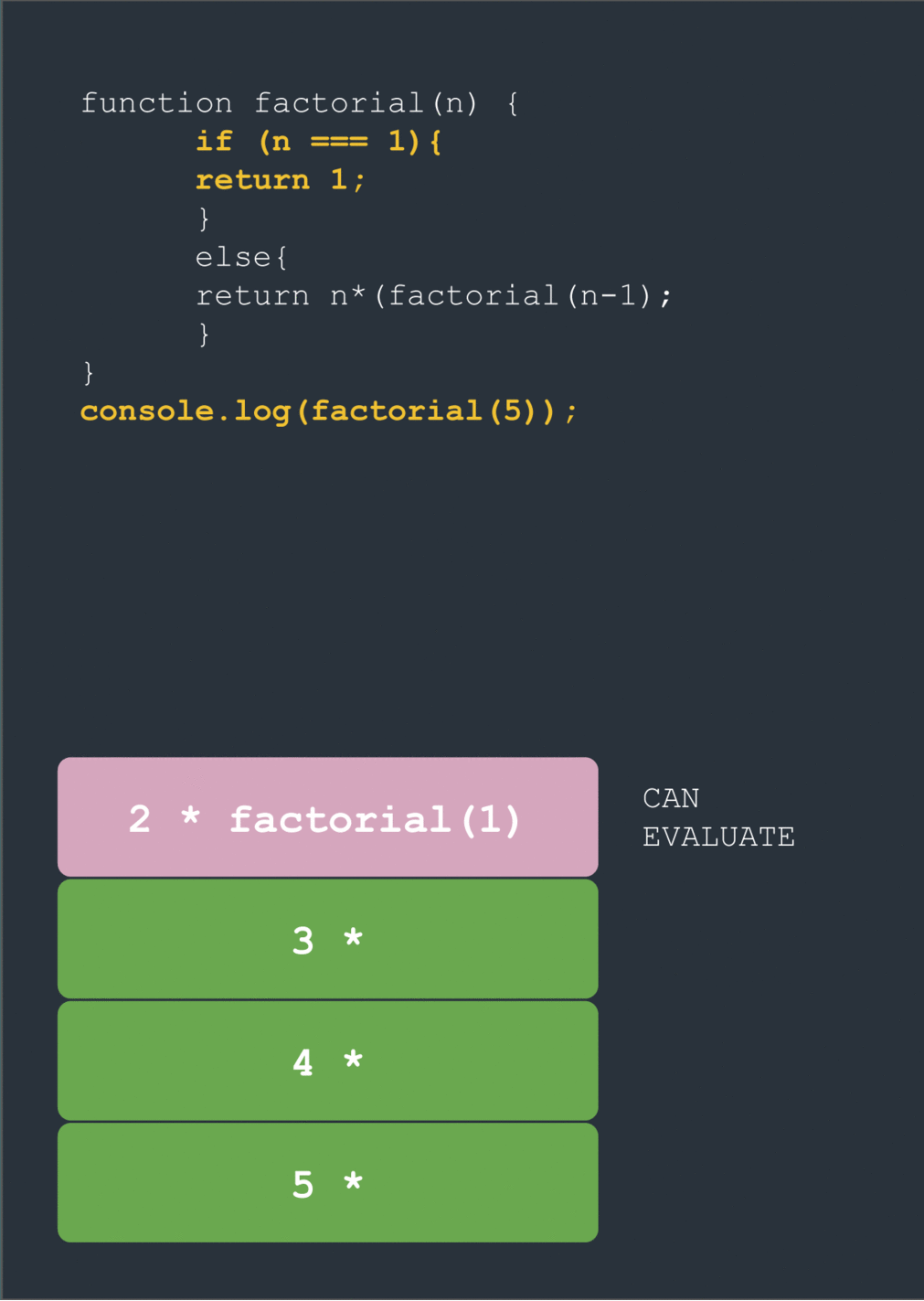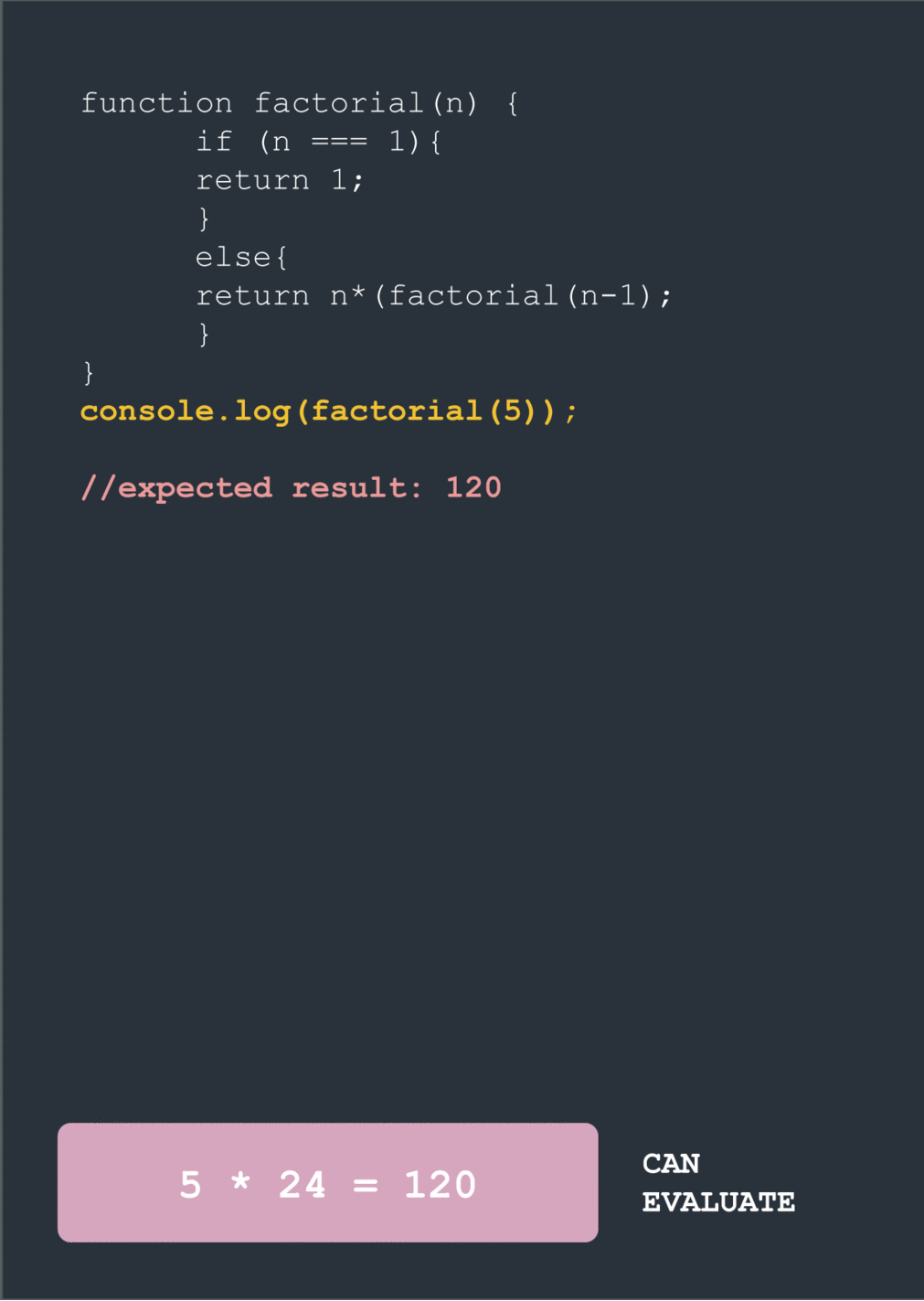
return 5 * factorial(4)
↓
// cannot evaluate!
At this point the universe should crack open because surely there’s no way to evaluate a function whose value is another function call! The solution is to keep going deeper: if factorial(5) can only be evaluated when we know the value of factorial(4) then we need to evaluate that too. If factorial(4) can only be evaluated when we know the value of factorial(3) … well you get it. We need to keep descending further and further until we hit something we can actually know the value of … which is where the break condition comes in.
When we hit factorial(1) we break out of the loop and finally return the value of 1. Now we can start the long climb back up to the top of this tree of nested function calls. Using our value for factorial(1) we can evaluate factorial(2) (2 * 1 = 2). This lets us evaluate factorial(3) (3 * 2 * 1 = 6). This then gives factorial(4), which then gives factorial(5).
factorial(5) = 5*---------------120 // finally!
↓ ↑
factorial(4) = 4*-------------24
↓ ↑
factorial(3) = 3*-----------6
↓ ↑
factorial(2) = 2*---------2
↓ ↑
factorial(1) = -----→---1
The analogy of “bubbling up” which I first came across in This video was a huge help in understanding how this kind of function works. When we have a whole tree of nested function calls waiting to be resolved, the bottom of the tree is where the chain of evaluations starts. As we successfully evaluate and close function calls, the result “bubbles” up to the top of the tree, eventually returning a result for our original function call.
This seems neat and tidy, but what happens when we move onto more complex recursive functions? Have a look at the range() function below:
function range(a,b){
if (b-a === 1){
return [];
}
else {
let list = range(a,b-1);
list.push(b-1);
return list;
}
}
This function returns the list of integers that fall between the values a and b, where a and b are both integers, and a < b. The expected result for range(2,9) would be [3,4,5,6,7,8].
The break condition for this function is b-a === 1 , since at this point there are no integers left between a and b so there’s nothing else for us to log as part of our result. Later, we’ll see why it’s essential here that we return an empty array rather than “0” or an empty string.
The recursive part of the function has three steps:
- Generate the variable
list - push a value onto
list - return
list
The tricky part here is in step 1: list needs to be assigned as range(a,b-1), which we haven’t yet evaluated. Like before, we are going to have to build a tree of nested functions, going deeper until we hit something we can evaluate; only at this point can we complete the original let list... instruction and assign the variable list.
Using range(2,6) as an example we would expect to get a tree like this:
range (2,6) → let list= -----[3,4,5] <<list.push(b-1)
↓ ↑
range (2,5)----------------[3,4] <<list.push(b-1)
↓ ↑
range (2,4)--------------[3] <<list.push(b-1)
↓ ↑
range (2,3)------→-----[] <<list gets assigned here!
Again, although we attempt to create list right at the top of the tree, we only complete that assignment right at the bottom. Only now can we move onto step 2, and start pushing values into list. Now it’s clear why we needed to return an empty array as part of the break condition: there wouldn’t be an array to push variables into if we didn’t define it here. Now we have our array, we can carry out step 2 for each of our nested function calls. Once this is done, we can finally move onto step 3, and return our completed list.
This order of progress is not entirely intuitive, so adding a couple of console.logs into the function body can help to clarify things:
function range(a,b){
if (b-a === 1){
console.log("two");
return [];
}
else {
console.log("one");
let list = range(a,b-1);
console.log("three");
list.push(b-1);
return list;
}
}
console.log(range(2,6));
//expected result
"one"
"one"
"one"
"two"
"three"
"three"
"three"
[3,4,5]
The “bubbling up” analogy from earlier really makes sense in this function. Intuitively we might expect the result [5,4,3] when we call range(2,6) since b = 6 is the first parameter we attempt to evaluate. Looking at the entire function tree we can see that we only start to push values into the array right at the bottom of the tree, filling the array in reverse order, from bottom to top.
“Bubbling up” is a really useful way to conceptualise recursive functions, but there’s an alternative way to look think about this with reference to the data structures at work under the hood while our function is running. When I run a script in my browser, it uses a call stack to keep track of which functions need to be called, and manage which function is being run at any particular time. The stack is a bit like a pile of dishes - items are constantly being taken off the top of the stack to tidy them away, and at the same time new items are added back on to the top. If a script is run with multiple function calls inside it, each of these will be evaluated and tidied away as necessary before progressing through the script. If a function call cannot be evaluated immediately, it stays on the bottom of the stack until we have the information we need to get a result. Have a look at this script:
function total(){
console.log(first()+second());
}
function first(){
return 5;
}
function second(){
return 6;
}
total();
First we call total(), but this cannot be evaluated until we’ve called first() and second(). So total() goes onto the bottom of the stack, while first() and second() are added above it. When first() and second() are evaluated we can clear them off the stack and pass their values into evaluate.
+---------+ +---------+
|second() | | = 6 |
+---------+ +---------+ +---------+
| first() | |first() | | = 5 |
+---------+ +---------+ +---------+ +---------+ +---------+
| total() | → | total() | → | total() | → | total() | → | = 11 |
+---------+ +---------+ +---------+ +---------+ +---------+
How does this work for a recursive function? There’s no difference really. Here’s an animation to demonstrate how the call stack manages the factorial() function from above: